내적(Dot Product)
내적은 두 벡터를 곱(multiplication)하는 연산이다.
내적은 scalar product 또는 inner product라고도 불린다.
### 정의
벡터 a, b의 요소가 주어졌을 때, 내적의 정의는 다음과 같다
$$a · b = a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$$
내적의 결괏값은 실수(real number)임을 기억하자.
또는 벡터 a와 b 사이의 각도가 주어졌을 때, 내적은 아래와 같이 계산할 수 있다.
$$a · b = ||a||\;||b||\;cos \theta$$
만약 두 벡터가 평행한 벡터라면, 두 벡터 사이의 각도는 0 또는 π 이다.
벡터의 내적공식을 변형하면 두 벡터 사이의 각을 구하는 것도 가능하다.
$$cos\theta = {a·b\over ||a||\;||b||}$$
응용하여 내적을 통해 둘 사이의 각이 예각/둔각/직각인지 여부도 판단할 수 있다.
### 연산법칙
내적 연산에 관련된 대표적인 성질 몇가지를 나열해두었다.
$$a·a\; =\; ||a||^{2}$$
같은 벡터에 대해 내적하면 그 크기의 제곱과 같다.
$$a·b \;=\; b·a$$
벡터의 내적에 대해서는 교환법칙이 성립한다.
$$a·(b+c)\; =\; (a·b)+(a·c)$$
분배법칙도 성립한다.
$$(da)·b\;=\;d(a·b) = a·(db)$$
d가 상수일 때, 결합, 교환법칙이 성립한다.
$$if\;\; a·b = 0,\;\;then \;orthogonal$$
벡터의 내적이 0이라면, 두 벡터는 직교한다.
### 방향각(direction angles)
방향각은 벡터 a가 각 축(x, y, z)와 이루는 각이다.
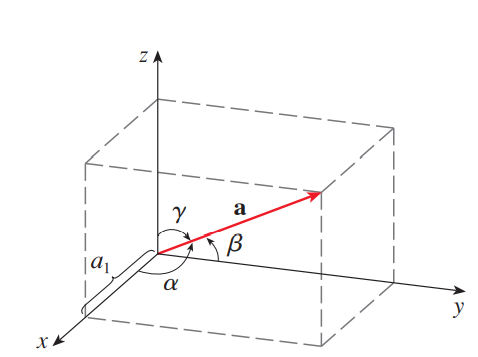
방향각은 벡터를 다음과 같이 표현함으로써 얻을 수 있다.
$$a\;=\;<a_{1},\;a_{2},\;a_{3}>\;=\;<a·i,\;a·j,\;a·k>\;=\;<||a||·||i||cos\alpha,\;||a||·||j||cos\beta,\;||a||·||k||cos\gamma>$$
$$a\;=\;<||a||cos\alpha,\;||a||cos\beta,\;||a||cos\gamma>\;=\;||a||<cos\alpha,\;cos\beta,\;cos\gamma>$$
$${1\over ||a||}a\;=\;<cos\alpha,\;cos\beta,\;cos\gamma>$$
벡터를, 그 벡터의 크기로 나누면 방향만 남는다는 개념으로 이해해보자.
a 벡터의 unit vector의 형태와 동일함도 상기하자.
### Projections(투사)
(1) vector projection
시작점이 같은 벡터 a, b가 있을때, b의 끝점에서 a 방향으로 수선의 발을 내리자.
시작점에서 그 수선의 발까지의 벡터를 다음으로 부른다.
vector projection of b onto a

projection은 벡터내적에 대한 다음의 논리로 유도할 수 있다.
$$a·b\;=\;||a||\;||b||\;cos \theta = ||a||\;(||b||\;cos\theta)$$
즉, 벡터의 내적은 (a벡터의 크기) * (a벡터에 투사된 b벡터의 크기) 로 해석할 수 있다는 것이 핵심이다.
위 식을 변형하면 다음과 같이 나타내어진다.
$$||b||cos\theta \;=\; {a·b\over ||a||}$$
투사된 벡터의 크기를 구했으니, 여기에 방향을 곱해주면 vector projection of b onto a를 구할 수 있다.
방향이 a의 방향과 같으므로 a의 방향, 즉 unit vector를 곱해주자.
$$proj_{a}b \;=\; ({a·b\over ||a||}){a\over ||a||}\;=\;{a·b\over ||a||^{2}}a$$
(2) scalar projection
scalar projection은 vector projection과 동일하나, 투사되어 만들어진 벡터의 크기(magnitude)를 일컫는 용어이다.

투사된 벡터의 크기만을 의미한다고 했으니, projection 식에서 크기만을 가져오면 된다.
$$comp_{a}b = {a·b\over ||a||}$$
### 일(work)에 대한 적용
F가 힘의 크기, D가 움직인 거리일 때, 일의 양 W는 다음과 같은 공식으로 구한다.
$$W\;=\;(||F||cos\theta)\;||D||\;=\;||F||\;||D||\;cos\theta\;=\;F·D$$
$$W\;=\;F·D$$
이때, 일의 단위는 J(줄)이다. (J = N·m)
외적(Cross Product)
외적은 벡터 a, b에 모두 수직인 '벡터' c를 의미한다.
$$a·c = 0\;\;and\;\;b·c = 0$$
내적이 real number였던 것과 달리 외적의 결괏값은 '벡터'이다.
### 정의
determinant의 측면에서 벡터의 외적 계산을 살펴보자.
$$a×b\;=\;<a_{1},\;a_{2},\;a_{3}>×<b_{1},\;b_{2},\;b_{3}>\;=\; \left| \begin{matrix} i&j&k \\ a_{1}&a_{2}&a_{3} \\ b_{1}&b_{2}&b_{3} \\ \end{matrix} \right|$$
$$\left| \begin{matrix}a_{2}&a_{3} \\ b_{2}&b_{3}\\ \end{matrix}\right| i \;-\;\left| \begin{matrix}a_{1}&a_{3} \\ b_{1}&b_{3}\\ \end{matrix}\right| j\;+\;\left| \begin{matrix}a_{1}&a_{2} \\ b_{1}&b_{2}\\ \end{matrix}\right| k$$
벡터 사이의 각을 안다면 다음과 같이 계산하는 것도 가능하다.
$$||a×b|| = ||a||\;||b||\;sin\theta$$
* 아래 그림을 통해, 두 벡터의 외적이, 두 벡터가 각각 변으로 구성된 평행사변형의 면적과 같음을 유추할 수 있다.

(밑변 × 높이 를 계산해보자.)
### 성질
외적의 연산과 관련된 여러 성질을 살펴보자.
외적은 벡터 a, b, c와 상수 d에 대해서 다음이 성립한다.
parallel if a×b = 0
두 벡터의 외적이 영벡터라면, 두 벡터는 평행하다.
i×j = k, j×i = -k
j×k = i, k×j = -i
k×i = j, i×k = -j
표준기저벡터 i, j, k에 대해서 위의 loop가 성립한다.
a×b ≠ b×a
(a×b)×c ≠ a×(b×c)
교환법칙과 결합법칙이 성립하지 않는다.
내적과 혼동하지 않도록 주의하자.
a × b = -b × a
외적의 교환이 이루어졌을 때 부호가 바뀐다.
(da) × b = d(a × b) = a × (db)
상수(d)에 대한 교환법칙과 결합법칙은 성립한다.
a × (b + c) = (a × b) + (a × c)
(a + b) × c = (a × c) + (b × c)
분배법칙이 성립한다.
a · (b × c) = a × (b · c)
(scalar triple product)외적과 내적이 섞여있을 때 성립한다. 외우자.
### Triple Product
아래와 같은 연산의 형태를 Scalar Triple Product라고 한다.
a · (b × c)
(b × c)를 한 덩어리로 보고 연산을 한다고 생각하면 쉽다.
아래를 읽으며 계산과정을 따라가보자.
$$a·(b×c)\;=\; \left| \begin{matrix} a_{1}&a_{2}&a_{3} \\ b_{1}&b_{2}&b_{3} \\ c_{1}&c_{2}&c_{3} \\ \end{matrix} \right|\;=\; \left| \begin{matrix}a_{2}&a_{3} \\ c_{2}&c_{3}\\ \end{matrix}\right| a_{1} \;-\;\left| \begin{matrix}b_{1}&b_{3} \\ c_{1}&c_{3}\\ \end{matrix}\right| a_{2}\;+\;\left| \begin{matrix}b_{1}&b_{2} \\ c_{1}&c_{2}\\ \end{matrix}\right| a_{3}$$
* 아래 그림을 통해, 두 벡터의 외적에 다른 벡터를 내적한 값이, 세 벡터를 변으로 가지는 평행육면체의 부피와 같음을 유추할 수 있다.

$$V\;=\;||a\;·\;(b\;×\;c)||$$
만약 Triple Product가 0이라면, 세 벡터가 모두 같은 평면(plane) 안에 있는 것으로 생각하자. ( volume = 0 )
$$a\;·\;(b\;×\;c)=0$$
### 외적의 적용: 돌림힘(Torque)
내적에서 끄는 힘, 미는 힘에 대한 적용공식이 있었다면 외적의 경우 돌림힘(torque)에 대한 공식을 적용할 수 있다.

돌리는 힘을 F, 돌리는 주체를 위치벡터(position vector) r, r과 F간의 각이 주어졌을 때, 돌림힘 t는 다음과 같이 구한다.
$$\tau = r × F$$
힘의 크기는 다음과 같이 구함을 유추가능하다.
$$||\tau|| = ||r × F|| = ||r||\;||F||\;sin\theta$$
'수학 > 미적분' 카테고리의 다른 글
| Cylinders & Quadric Surfaces (0) | 2022.02.05 |
|---|---|
| 선(Lines), 평면(Planes)의 방정식(Equations) (0) | 2021.10.19 |
| 3차원 좌표계와 벡터(vector) (0) | 2021.10.19 |
| 테일러 급수(Taylor Series)와 맥클로린 급수(Maclaurin Series) (0) | 2021.10.17 |
| 멱급수(Power Series) (0) | 2021.10.01 |