3차원 좌표계에 대한 이해
2차원에서 다루는 curve가 3차원좌표계로 넘어갔을 때는 면(surface)이 된다.
또한, 2차원에서 다루는 면이 3차원좌표계로 넘어갔을 때는 입체(solids)가 된다.
예를 들어보자.
$$y = 5,\;\; in\;\; R^{3}$$

2차원에서는 직선이었을 식이 3차원좌표계로 넘어가 면(surface)이 되었다.
다른 예로 입체또한 이해해보자.
$$x^{2}+y^{2} = 1 \;\;in\;\;R^{3}$$
2차원에서 보면 중심이 원점이고 반지름이 1인 원이다.
3차원에서 보면, 속이 비어있는 원기둥(cylinder)이 된다.
이때, z의 제한이 주어져있지 않기 때문에, 원기둥의 길이는 아래위로 무한대이다.

다음과 같은 범위가 주어졌을 때는 조금 달라진다.
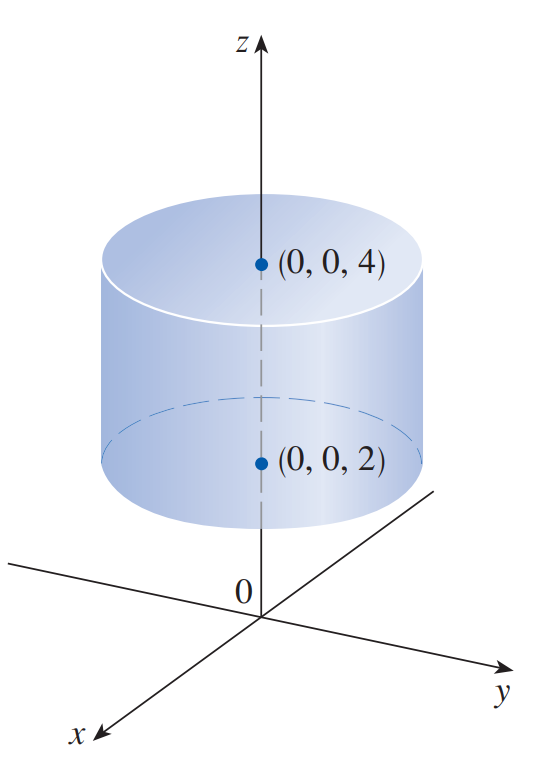
$$x^{2}+y^{2} ≤1,\;\; 2≤z≤4$$
부등식으로 인해 원기둥의 속이 차있는 'solid'일 것이고, z의 범위가 주어졌기 때문에 아래와 같은 그림이 나올 것이다.
3차원에서의 거리(distance)와 구(spheres)
2차원에서와 비슷하게, 3차원좌표계에서의 두 점 사이 거리는 다음과 같이 구한다.
$$|P_{1}P_{2}| = \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}$$
중심이 C(h, k, l)이고 반지름(radius)이 r인 3차원 좌표계에서의 구(sphere)의 방정식은 다음과 같다.
$$(x-h)^{2}+(y-k)^{2}+(z-l)^{2} = r^{2}$$
벡터와 벡터의 기본개념
벡터는 크기(magnitude)와 방향(direction)을 함께 지닌 것을 수학적으로 표현할 때 사용한다.
주로 화살표(→)를 사용해서 표현하며, 크기는 그 길이로 나타내고 방향은 화살표가 가리키는 방향으로 나타낸다.
벡터의 시작점, 끝점의 위치와 관계없이 크기와 방향만 같으면 동일한 벡터라고 이해하자.
### 벡터의 덧셈
두 벡터 u, v의 합 u+v를 표현하고자 할 때 두 가지 방법을 사용할 수 있다.
(1) Triangular Law
한 벡터의 끝과 다른 벡터의 시작이 연결되어있을 때, 두 벡터의 합은 한 벡터의 시작에서 다른 벡터의 끝을 직선으로 연결한 벡터를 만들어 구할 수 있다.

(2) Parallelogram Law
시작점이 같은 두 벡터에 각각 평행한 벡터를 만들어 형성된 평행사변형을 이용해 합을 구하는 것도 가능하다.
그림으로 이해해보자.

### 벡터의 상수배
벡터 v에 상수 c를 곱해 cv를 만든다고 치면, v벡터의 길이가 c배로 늘어난다고 이해하면 된다.
c = 2라면 길이, 즉 magnitude가 2배가 되는 것이고, c가 음수라면 벡터의 방향이 반대로 뒤집어질 것이다.
이를 응용하면 u-v, 즉, 벡터의 뺄셈이 결국 u 벡터와 -v 벡터의 합임을 유추할 수 있다.
벡터의 요소(components) 면에서 벡터 이해하기
### 위치벡터(position vector)
3차원 좌표에서 점 P의 좌표가 다음과 같이 주어졌다고 치자.
$$P(a_{1},\;a_{2},\;a_{3})$$
이때, 원점에서부터 점 P까지를 연결하여 만든 벡터 a를, 점 P에 대한 positon vector(위치벡터)라고 한다.
$$a = <a_{1},\;a_{2},\;a_{3}>$$
### 두 점의 좌표가 주어졌을 때 벡터 표현법
위치벡터가 원점-점P까지를 연결해서 만든 벡터임을 응용하면, 두 점의 좌표가 주어졌을 때 둘을 연결해 벡터를 만드는 것도 가능하다.
3차원 좌표에서 점 A와 점 B의 좌표가 다음과 같이 주어졌다고 치자.
$$A(x_{1},\;y_{1},\;z_{1}),\;\;B(x_{2},\;y_{2},\;z_{2})$$
이때, 벡터 AB는 다음과 같다.
$$\overrightarrow{AB} = <x_{2}-x_{1},\;y_{2}-y_{1},\;z_{2}-z_{1}>$$
### 벡터의 크기(magnitude)
벡터의 요소가 주어졌을 때, 해당 벡터의 크기, 즉 길이는 다음과 같이 구한다.
$$||a|| = \sqrt{a_{1}^2+a_{2}^2+a_{3}^2}$$
### 벡터의 연산성질
벡터 a, b, c와 상수 d, e가 주어졌을 때, 다음과 같은 연산법칙이 성립함을 알아두자.
(1) a+b = b+a
벡터의 덧뺄셈은 교환법칙이 성립한다.
(2) a+(b+c) = (a+b)+c
결합법칙도 성립한다.
(3) d(a+b) = da+db
상수(scalar)에 대한 분배법칙이 성립한다.
기저벡터 (basis vector)와 단위벡터(unit vector)
### basis vector
다음의 벡터들을 보자.
$$i = <1,0,0>,\;j = <0,1,0>,\;j = <0,0,1>$$
이와같은 벡터들을 표준기저벡터(standard basis vector)라고 한다.
표준기저벡터는 다음의 성질을 지닌다.
1. 크기(magnitude)가 1이다.
2. 각 좌표축(axes)의 양의 방향(positive direction)을 가리킨다.
기저벡터로 일반벡터를 표현하는 것도 가능하다.
$$a \;=\; <a_{1}, a_{2}, a_{3}> = a_{1}i \;+\;a_{2}j\;+\;a_{3}k$$
### unit vector
단위벡터는 크기가 1인 벡터를 의미한다.
위의 표준기저벡터 i, j, k 모두 단위벡터에 해당한다.
일반적으로, 벡터 a가 영(0)벡터가 아닐 때, 단위벡터는 a의 방향과 동일한 방향을 지닌다.
단위벡터를 구할 때는, 아래와 같이 벡터를, 그 벡터의 크기로 나눠준다.
$$u \;=\; {1\over ||a||}a\; = \;{a\over ||a||}$$
예시로 단위벡터를 구하는 방법을 이해해보자.
다음 벡터의 단위벡터를 구하는 것이 목표다.
$$2i-j-2k$$
단위벡터의 크기부터 구하자.
$$||2i-j-2k|| = \sqrt{2^{2}+(-1)^{2}+(-2)^{2}} = \sqrt{9} = 3$$
구한 크기를 벡터에 나눠주면 된다.
$${1\over 3}(2i-j-2k)\;=\;{2\over 3}i-{1\over 3}j-{2\over 3}k$$
'수학 > 미적분' 카테고리의 다른 글
| 선(Lines), 평면(Planes)의 방정식(Equations) (0) | 2021.10.19 |
|---|---|
| 벡터의 내적(dot product)과 외적(cross product) (0) | 2021.10.19 |
| 테일러 급수(Taylor Series)와 맥클로린 급수(Maclaurin Series) (0) | 2021.10.17 |
| 멱급수(Power Series) (0) | 2021.10.01 |
| 급수(Series)와 그 극한 (0) | 2021.09.30 |