SVM (Support Vector Machine)이란😶
SVM도 이전에 정리했던 Logistic Regression처럼 이진분류모델이다.
SVM 작동원리를 차근차근 살펴보자.
✔️최적의 Hyperplane을 찾자 = SVM!
데이터가 주어졌을 때, Hyperplane을 그어 이를 두가지로 나누는 방법에는 여러가지가 있다.
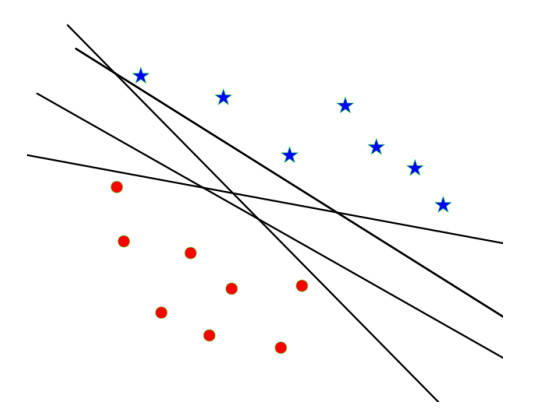
그림처럼, 같은 데이터를 분류한다고 하더라도 서로 다른 파라미터 조합으로 만든 여러개의 Hyperplane이 존재할 수 있다.
수많은 Hyperplane 중에서 가장 최적의 것을 찾는 것이 문제다.
SVM은 이 '최적'의 모델을 '데이터와 Hyperplane 간의 Margin이 최대가 되는 Hyperplane' 이라고 보는 것이 핵심이다.
그림으로 좀 더 명확히 살펴보자.

Hyperplane과, 데이터 중 가장 가까운 점들 간의 거리가 margin으로 표시되어있음을 확인할 수 있다.
나중에 데이터가 더 들어왔을 때, Hyperplane이 해당 데이터에 대해서도 분류를 잘 하기 위해서는 지금 훈련데이터를 기준으로 만든 hyperplane과 데이터 간 거리가 최대한 멀어야 할 것이다.
따라서, SVM은 'Margin의 크기가 최대가 되도록 하는 모델'로 이해하면 되겠다.
수식으로도 margin을 표현해보자.
위 그림에서, hyperplane을 중심으로 거리가 1인 두 데이터 X_pos와 X_neg가 있다.
각 점을 지나고 Hyperplane과 평행한 선들을 아래와 같다.
$$\begin{cases} w_{0}+w^{T}x_{pos} = 1 \\ w_{0}+w^{T}x_{meg} = -1 \end{cases}$$
또한, x_pos와 x_neg간의 거리는 λw이다.
$$x_{pos} = x_{neg}+\lambda w$$
이 세 식을 연립하면 람다를 다음과 같이 정리할 수 있다.
$$\begin{cases}w_{0}+w^{T}(x_{neg}+\lambda w) = 1 \\ w_{0}+w^{T}x_{neg} = -1 \end{cases}$$$$-1+\lambda w^{T}w = 1$$$$\lambda = {2 \over w^{T}w}$$
정리된 람다를 활용해 margin을 구하면 다음과 같은 전개가 이어진다.
$$Margin \ = \ distance(x_{pos}, x_{neg}) \ = \ ||x_{pos}-x_{neg}||_{2} \ = \ ||\lambda w||_{2} \ = \ \lambda \sqrt{w^{T}w} \ = \ {2\over ||w||_{2}}$$
즉, SVM은 아래를 가장 크게 하는 Hyperplane을 구하는 모델이라고 정리할 수 있다.
$${2 \over ||w||_{2}}$$
다르게 말하면, 아래 식을 최소가 되도록 하는 w_0, w를 구하는 것이 SVM이다.
$$||w||_{2}\over 2$$
SVM의 Loss Function 정리😶
위에서 SVM은 margin의 크기를 최대화하는 모델이라고 했다.
정확히 이야기하면 아래 두 가지를 만족하는 모델이다.
✨Margin의 크기가 최대가 되도록 하면서 (Regularlization)
✨Loss를 최소화 하는 모델
margin을 최대화하는 것에 대해서는 위에서 설명했다.
남은 것은 Loss Function인데, SVM은 Hinge Loss를 Loss Function으로 둔다.
$$L_{H}(\hat{y}, \ y) = max(0, \ 1-\hat{y}y)$$
$$L_{H}(\hat{y}, \ y) = max(0, \ 1-y^{(i)}(w_{0}+w^{T}x^{(i)}))$$
Loss가 음수인 경우는 없기 때문에, loss의 최소를 0(예측을 정확히 한 경우)이라고 두고 1에서 실제값*예측값을 곱한 것을 뺀 값 중 큰 것을 선택하는 식으로 Loss Function이 짜여있음을 확인할 수 있다.
Soft Margin SVM😶
실제 데이터를 분류하는 상황에서 SVM이 어떻게 동작하는 것이 맞는지, 단계별로 알아보자.
✔️시도1
Naive한 접근법이다.
모든 점 i에 대해 다음을 만족하는 w, w0을 구하는 방법이다.
$$y^{(i)}(w_{0}+w^{T}x(i)) ≥ 1$$
실제 y 값과 예측값 y의 곱이 1보다 크거나 같도록 Hyperplane을 긋는 논리다.
✔️시도2 (Soft-Margin SVM)
시도1이 언제나 잘 작동하면 좋겠지만, 데이터가 선형으로 깔끔하게 완전히 나뉘는 경우는 드물다.

그림처럼, Hyperplane을 그었을 때 제대로 분류되지 않는 데이터(slack)가 있기 마련이다.
이때는, 이러한 slack을 어느정도 허용해주는 작업이 필요하며, 이러한 허용을 반영한 SVM을 Soft Margin SVM이라고 부른다.
slack의 허용에는 아래 두 가지 방법이 있다.
✨ε
slack variable이다.
실제값과 예측값의 곱이 1보다 작아지는 것을 허용해주는 역할을 한다.
$$y^{(i)}(w_{0}+w^{T}x(i)) ≥ 1-\epsilon_{i}$$
위의 naive 식과 비교하면서 이해하자.
✨γ
slack을 얼마나 허용해줄 것인지를 컨트롤하는 Hyperparameter다.
Loss Function에 Hyperparameter 감마(γ) 를 붙여주면 된다.
커질수록 hard margin의 속성을 띠며, 0이 될 경우 모든 slack을 다 허용하게 된다.
총정리😶
Regularlization, Loss Function, 그리고 slack의 허용까지 반영한 SVM은 수식으로 다음과 같이 나타낼 수 있다.
$$argmin_{w,w_{0},\epsilon}\sum_{i=1}^{N}max(0, \ 1-y^{(i)}(w_{0}+w^{T}x^{(i)})) \ + \ {||w||_{2}\over 2\gamma}$$
$$where \ \ y^{(i)}(w_{0}+w^{T}x(i)) ≥ 1-\epsilon_{i}$$
Loss Function(hinge loss)이 최소가 되도록 하는 w, w0 등을 구하며, 뒤에 Regularlization또한 반영되어있음을 확인하자.
(+) 위에서 감마를 Loss Function에 붙인다고 했는데, 위 식에서는 Regularlization의 분모에 붙은것을 확인하자.
(계산을 위해 분모로 옮겨준 것.)
'Data Science > ML | DL' 카테고리의 다른 글
| [Pytorch] Classification 모델 구현하고 MNIST 데이터로 훈련하기 (0) | 2022.08.15 |
|---|---|
| Multi-Class Classification에서 Softmax Function을 쓰는 이유 (0) | 2022.08.15 |
| [머신러닝] Logistic Regression으로 Binary Classification 감 잡기 (0) | 2022.08.13 |
| [머신러닝] Loss Function과 Cost Function (0) | 2022.08.13 |
| [머신러닝] 까먹으면 안되는 K-NN 이론 (0) | 2022.08.13 |