Logistic Regression은 대표적인 Binary Classifier 중 하나다.
(이름은 Regression인데 분류모델이다.)
Parametric Model 접근법😶
이전에 포스팅했던 모델은 Non-Parametric Model인 K-NN이었다.
여기서 포스팅할 Logistic Regression은 Parametric Model이다.
Logistic Regression이전에, Parametric Model을 다룰 때 어떻게 접근하는지 살펴보자.
Parametric Model과 Non-Parametric Model의 차이는 아래 링크를 타고 들어가 확인할 수 있다.
2022.08.12 - [Data Science/ML | DL] - 까먹지 않아야 할 머신러닝의 아주 기본
까먹지 않아야 할 머신러닝의 아주 기본
머신러닝(Machine Learning)이란😶 새로운 데이터를 잘 맞추는 모델을 데이터로부터 구축하고 학습시키는 것이다. Data-Driven Approach, Supervised Learning이라고도 불린다. (정답이 있는 데이터를 학습시키
dippingtodeepening.tistory.com
아래는 Parametric Model 접근법의 간단한 단계이다.
✔️1. 모델 고르기
✔️2. Loss Function 정의
✔️3. Prior Knowledge에 기반해 Regularizer 선택
✔️4. Optimization Algorithm을 사용해 모델 fit하기
앞으로 Parametric Model은 위 과정을 통해 훈련되는 것을 확인할 수 있을 것이다.
Linear Classifier부터 Logistic Regression까지😶
결론부터 말하면, Logistic Regression은
Loss Function으로서 cross-entropy를 사용하고,
Activation Function으로 sigmoid function을 사용하여
두 개의 label을 분류하는 모델이다. (Binary Classification)
이렇게만 알아도 괜찮지만, 왜 Loss Function과 Activation Function을 해당 함수들을 사용하는지 그 이유를 아래 단계로 이해했던 것이 원리 이해해 많은 도움이 되어 여기 정리한다.
✔️ Linear Classifier
먼저 Linear Classifier를 이해해야 Logistic Regression을 사용하는 이유를 알 수 있다.
Perceptrone이라고도 불리는 Linear Classifier는, 말 그대로 데이터를 직선형으로 분류하는 모델을 의미한다.
수식으로 나타내면 아래와 같겠다.
$$f(x;w) = w_{0}+w^{T}x$$
여기서 w와 w_0은 모델 parameter (w는 weight, w_0은 bias라고 불림)이고, 이렇게 파라미터와 input의 조합 결과를 만들어내는 함수 f를 activation function이라고 한다.
✔️시도 1
아래 데이터를 두 class로 분류하는 것이 문제로 주어졌다고 치자.

Linear Classifier가 사용되는 것이 일단 적절해보인다.
시도 1에서는 Activation Function, Loss Function은 다음과 같이 설정되었다.
$$\hat{y}=\begin{cases}1\ \ \ \ \ if \ f(x;w)≥0 \\ -1 \ \ \ \ \ otherwise \end{cases}$$
적절한 decision rule을 설정한 모습이다.
0을 중심으로 부호가 양수이면 -1, 음수이면 1로 y 예측값을 정하면 분류될 것이다.
✨Activation Function
부호로 y 예측값을 정하기 때문에, Activation Function은 '부호'가 될 것이다.
$$\hat{y}=sign(w_{0}+w^{T}x)$$
✨Loss Function
$$L_{0-1}(\hat{y},y) = \begin{cases} 0 \ \ \ \ \ if \hat{y}=y \\ 1 \ \ \ \ \ if \hat{y}≠y \end{cases} = I[\hat{y}≠y]$$
시도1에서는 예측값과 값이 일치하면 Loss가 1, 아니면 0인 것으로 정한 것을 확인할 수 있다.
시도1에서 발생할 수 있는 문제점들은 다음과 같은 것들이 있다.
1. NP Hard Problem
Loss Function을 '일치여부'로 계산했기 때문에, 무엇을 틀렸는지는 알 수 없는 문제가 있다.
2. Discontinuity
Loss Function을 그려보면 불연속이다.
이는 미분이 안된다는 이야기인데, 미분이 안된다는 말은 gradient를 구할 수 없다는 말과 같다.
(Gradient Descent 등을 통한 파라미터 Optimization이 불가능함.)
✔️시도 2
시도1에서 발생하는 문제를 해결하기 위해, 시도2에서는 다음과 같이 Loss Function과 Activation Function을 수정된다.
✨Activation Function
$$\hat{y} = w_{0}+w^{T}x$$
activation 함수가 '부호'가 아닌, 값 자체로 바뀌었다.
✨Loss Function
$$L_{SE}(\hat{y},y) = {1\over 2}(\hat{y}-y)^{2}$$
Square Error의 형태로 Loss Function이 정의되었음을 알 수 있다.
분류하면 아래와 같은 형태가 될 것이다.

시도2는, 시도1의 문제를 일부 개선했지만 '답이 맞음에도 불구하고 loss가 큰 상황'을 발생시킬 수 있다는 치명적인 단점이 있다. (correct prediction with high confidence)
y를 -10이라고 확신하여 예측했을 때, y의 실제값이 -1이어 classification의 개념에서 올바른 분류를 했음에도 불구하고 loss가 크게 계산되는 상황을 생각하면 이해하기 쉽다.
✔️시도 3
시도2의 한계는 Activation Function이 Linear Classifier 형태로 정의되었기 때문에 발생한다.
따라서 시도 3에서는 Activation Function을 다음과 같이 바꿔준다.
✨Activation Function
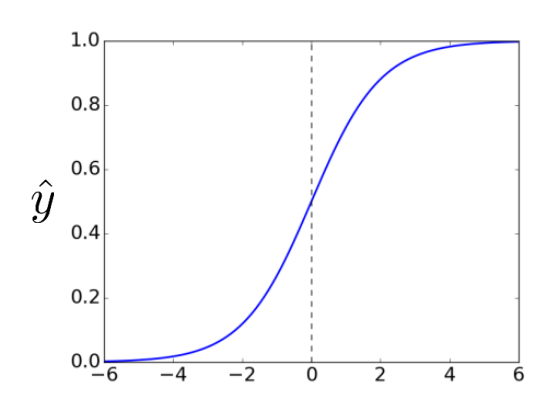
$$\hat{y}=\sigma (w_{0}+w^{T}x)$$
activation function이 sigmoid 함수임을 알 수 있다. (logistic function이라고도 불림)
예측값이 -1에서 1의 범위를 넘지 않도록 해 orrect prediction with high confidence가 없도록 한다.
(Logistic Regression의 형태에 가까워지고 있다.)
아래는 logistic function의 형태이다.
✨Loss Function
$$L_{SE}(\hat{y},y) = {1\over 2}(\hat{y}-y)^{2}$$
Loss Function은 시도2와 동일하다.
이렇게 하면 시도2의 한계였던 correct prediction with high confidence는 해결된다.
하지만 '예측이 완전히 틀렸을 때', 즉 실제값과 너무 상이한 값으로 예측했을 때의 loss가 더 커지지 않는 문제점이 새로 생기게 된다.
✔️시도 4 (Logistic Regression)
시도4에서는 Loss Function을 바꿔준다.
✨Activation Function
$$\hat{y}=\sigma (w_{0}+w^{T}x)$$
시도3과 동일하다.
✨Loss Function
$$L_{CE} \ = \ -y \ log \hat{y}-(1-y) \ log(1-\hat{y})$$
Loss Function을 cross entropy의 형태로 바꿔주어, 예측이 '완전히' 틀렸을 때의 loss가 기하급수적으로 증가하도록 개선한 것을 확인할 수 있다. (y와 y hat에 다른 값을 넣어보자.)
이러한 형태의 모델이 Logistic Regression이며, 이것이 왜 Logistic Regression을 쓰는 이유를 설명해준다.
부가적으로 위의 entropy 형태의 Loss를 계산할 때, divide by zero 현상이 일어날 것을 대비하여 아래와 같이 형태를 변형하여 쓰는 것이 좀 더 완성된 형태이다.
$$L_{LCE}(z,y) \ = \ L_{CE}(\sigma(z),y) \ = \ y \ log(1+e^{-z})+(1-y) \ log(1+e^{z})$$
'Data Science > ML | DL' 카테고리의 다른 글
| Multi-Class Classification에서 Softmax Function을 쓰는 이유 (0) | 2022.08.15 |
|---|---|
| [머신러닝] SVM으로 Binary Classification 다지기 (0) | 2022.08.14 |
| [머신러닝] Loss Function과 Cost Function (0) | 2022.08.13 |
| [머신러닝] 까먹으면 안되는 K-NN 이론 (0) | 2022.08.13 |
| Overfitting과 Underfitting, 그리고 Bias-Variance Trade Off (0) | 2022.08.12 |