Candidate Generation 과정 없이 Frequent Pattern을 추출해낼 수 있는 방법이 FP-Growth라고 했다.
local frequent pattern item을 사용하여 짧은 패턴부터 시작해, 패턴을 늘려가는 것이 FP(frequent pattern)-growth다.
Construct FP-Tree from Database
FP-Growth를 이해하기 전에, FP-Tree를 만드는 방법을 먼저 알아보자.
1. single item pattern 찾기
우선, DB를 스캔해 길이가 1짜리인 item pattern을 찾는다.
아래 그림에서 frequent items의 요소 하나 하나가, 길이 1짜리 item pattern이다.
2. F-list 만들기
찾은 frequent pattern을 빈도가 높은 것에서 낮은 것 순서대로 배열한다.
이렇게 만든 리스트를 F-list라고 한다.

F-list = f-c-a-b-m-p
f-list는 위와 같을 것이다. (세보자.)
3. Local FP-Tree 만들기
DB를 다시 scan하고, FP-Tree를 만든다

이전에 fp-tree가 존재하지 않았기 때문에, root 부터 차례로 F-list의 요소를 하나씩 넣어주면 된다.
4. FP-Tree 업데이트해 Global FP-Tree 만들기
가장 첫 번째 transaction의 frequent pattern에 대해서 FP-Tree를 만들었다.
다음으로 할 일은 다음 transaction를 기반으로 FP-Tree를 업데이트 해주는 것이다.
두 번째 transaction의 frequent item이 f,c,a,b,m이므로, root 부터 차례로 요소를 하나씩 업데이트해주면 된다.
f, c, a의 경우 루트에서 찾을 수 있으므로, 노드를 추가할 필요 없이 기존 노드의 frequency를 1에서 2로 늘려주기만 하면 된다.
b는 기존 route 상에 존재하지 않으므로 새로운 자식노드 b를 만들어주면 되며, m은 b의 자식노드로 새로 만들어주면 된다.
이러한 과정을, 모든 item에 대해서 반복해주면, Local FP-Tree가 Global FP-Tree로 업데이트 된다.
최종 결과는 아래와 같을 것이다.

이 때, linked list가 같은 item pattern을 연결해주고 있음에 유의하자.
FP-Tree Structure의 이점
[Completeness]
우선 정보에 손실이 없다.
버려지는 정보 없이, 완전한 정보(complete information)를 보호할 수 있다.
[Compactness]
frequent 하지 않은 item을 없애버림으로써 간단해지는 이점도 있다.
또한, 빈도 내림차순으로 item을 정렬하여 f-list를 만드는 과정으로, 노드를 여러 개 만들 필요 없이, 빈도가 높은 item이 같은 노드로 공유되도록 만들었다.
즉, 메모리에서 처리가 가능해질 정도로 정보를 저장하는 구조의 크기를 줄일 수 있다는 점이 이점이다.
이렇게 되면 DB에 접근할 필요가 없어지게 되고, 메모리에 업로드가 가능해진다.
FP-Growth
FP-Tree를 만드는 방법을 이해했으니, FP-Growth의 과정을 이어 이해해보자.
위에서 언급했듯이, local frequent pattern item을 사용해, 짧은 패턴부터 시작하여 패턴을 늘려가는 것이 개괄이다.
순서는 아래와 같다.
1. 각 frequent item에 대해, conditional pattern-base와 그 conditional FP-Tree를 만든다.
2. 새로 만들어진 FP-Tree에 대해 과정 1을 반복한다. (Recursively Repeating. Divide & Conquer)
3. 결과로 나오는 conditional FP-Tree가 비어있거나({ }) 길이 하나 뿐이면(single path), 해당 FP-Tree에 대한 반복을 종료한다.
즉, conditional pattern-base로 conditional FP-Tree를 만드는 것을 반복하여 최종 frequent pattern을 찾는 것이 FP-Growth라고 이해하면 될 것이다.
예시를 따라가며 순서대로 살펴보자.
F-List는 위에서 만든 FP-Tree에서와 마찬가지로, f-c-a-b-m-p라고 하자.
conditional pattern-base는, 이 F-List의 가장 끝부터 만들기 시작한다.
즉, 가장 frequent하지 않은 요소부터 시작해서 conditional pattern-base를 만드는 것으로 이해하면 되겠다.
(FP-Tree를 만들 때, 가장 빈도가 높은 요소부터 root에 집어넣는 것과 반대다.)
p conditional pattern base (p가 포함된 pattern)
m conditional pattern base (m이 포함되었으나 p가 포함되지 않은 pattern)
b conditional pattern base (b가 포함되었으나 p, m이 포함되지 않은 pattern)
...
f conditional pattern base (f가 포함되었으나, 나머지가 포함되지 않은 pattern)
순으로 만드는 것이 순서일 것이다.
우선 p conditional pattern base (p가 포함된 pattern)를 만드는 것을 시작으로 하자.
완성된 Global FP-Tree의 linked list를 따라 p를 찾고, p를 따라 root까지 올라가 패턴을 찾는다.

찾은 p와 연결된 패턴은 다음 두 가지다.
p => fcam:2, cb:1
이것들이 p conditional pattern-base이며, 각각의 숫자는 pattern base 아래의 p의 수와 동일하다.
conditional pattern-base를 만들었으므로, 그를 기반으로 하는 conditional FP-Tree를 만드는 것이 다음 단계이다.
이번엔 m-conditional pattern base를 기반으로 m-conditional FP-Tree를 만드는 시점이라 치고 따라가보자.
위 Global Tree를 바탕으로 보았을 때, m conditional pattern-base는 아래와 같다.
m => fca:2, fcab:1
FP-Tree를 만들기 위해서 우선 이 pattern base를 DB로 만들자.
| f c a |
| f c a |
| f c a b |
pattern base의 수만큼 쌓아서 DB를 만들어주면 된다.
이제부터는 위에서 설명한 FP-Tree를 만드는 방식과 동일하다.
MinSup이 3으로 주어졌다고 했을 때, 이 DB에서 b는 3개가 안되므로 각 행의 frequent item은 아래와 같이 필터링된다.
| {f c a} |
| {f c a} |
| {f c a |
이제 알던 대로 행 순서대로 root에서부터 각 요소의 frequency를 높여주며 FP-Tree를 만들면 된다.
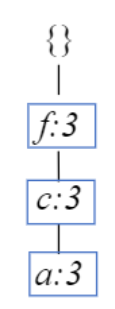
이것이 m conditional FP-Tree가 될 것이다.
이제 만들어진 conditional FP-Tree에 대해 다시 conditional pattern base를 만들어주면 된다.
다시, F-list는 이제 f-c-a이다.
가장 빈도가 낮은 a conditional pattern-base를 찾자.
엄밀히 말하면 am conditional pattern-base이다. (아직 m 의 recursion이 끝나지 않았다.)
am => fc: 3
찾았다. 마찬가지로, 이번엔 am conditional FP-Tree를 만들자.
| f c |
| f c |
| f c |

이것이 am conditional FP-Tree가 될 것이다.
이어서 cam conditional, fcam confitional FP-Tree를 만들어야 할 것이다.
그렇게 되면 FP-Tree가 빈 상태({ })가 된다.
이제, fcam conditional FP-Tree의 recursion을 빠져나오면 된다.
정리하면 m이 들어있는 frequent pattern을 추출하는 과정은 아래와 같은 순서로 진행된다.
{m}->{am}->{cam}->{fcam}->recursion 빠져나오기->recursion 빠져나오기->{fam}->recursion 빠져나오기->recursion 빠져나오기->{cm}->{fcm}->recursion 빠져나오기->recursion 빠져나오기->{fm}->recursion 빠져나오기->recursion 빠져나오기->끝
결과적으로, m conditional frequent pattern들은 다음과 같을 것이다.
{m} {am} {cam} {fcam} {fam} {cm} {fcm} {fm}
같은 방식으로, a conditional frequent pattern, c conditional frequent pattern, f conditional frequent pattern을 만들면 된다.
FP-Tree가 Single Prefix Path인 경우
위에서 conditional FP-Tree를 만들었을 때, 길이 하나인 경우가 있었다.
이런 경우에 해당하는 경우, (상부) 일직선을 노드 하나로 만들어 FP-Growth를 진행해주면 과정이 단순해진다.
아까 m-conditional frequent pattern의 경우, recursion 과정 필요 없이 2^3 개(f,c,a 3개)의 패턴을 바로 찾을 수 있을 것이다.
FP Growth VS Apriori
Apriori와 비교했을 때 FP Growth가 지니는 이점은 무엇일까.
우선 candidate generation이 없기 때문에 Minimum Support 값이 작아질 수록, apriori에 비해 속도가 빨라진다.
Divide-Conquer 방식이므로 큰 문제를 작은 문제로 쪼개는 데에서 오는 이점도 있다.
그 밖에도 아래의 이점들이 존재한다.
Candidate Generation, Candidate Test가 없다.
DB에 여러 번 접근하지 않고 메모리에서 해결 가능하다.
DB scan 횟수가 두 번 뿐이다. (처음 길이 1짜리 frequent 확인용 / Global FP-Tree 만들 때)
계산이 간단하다.
'Data Science > Mining' 카테고리의 다른 글
| Vertical Data Format으로 FP 찾기: CHARM (0) | 2022.04.17 |
|---|---|
| Mining Max-Pattern, Mining Closed Pattern (0) | 2022.04.01 |
| Improving Apriori (0) | 2022.04.01 |
| Apriori 알고리즘 (0) | 2022.03.31 |
| Frequent Pattern Analysis의 기본 개념 (0) | 2022.03.25 |