[ Downward Closure Property ]
어떤 itemset이 frequent하다면, 그 모든 subset들이 무조건 frequent하다는 것을 의미한다.
예를 들어, {beer, diaper, nuts}가 frequent하다는 결론이 나면, 그 subset인 {beer, diaper}은 당연히 frequent하다는 규칙으로 이해하면 되겠다.
* 그 대우도 성립하는 것을 확인할 수 있다.
(subset이 frequent하지 않으면, 그 super-set도 frequent할 수 없다.)
이전에 포스팅했던 내용이다.
Apriori 알고리즘은, 이러한 규칙을 기반으로 frequent 패턴을 추출하는 알고리즘으로 이해하면 되겠다.
[ Apriori Pruning Principle ]
infrequent한 itemset이 있다면, 그 superset은 절대 frequent하지 않다.
위의 Downward Closure Property의 대우와 맥락이 같은 것을 확인할 수 있다.
Apriori의 방법
Apriori의 알고리즘이 어떻게 돌아가는 지 알아보자.
아래는 그 대략적인 순서다.
1. DB를 한 번 스캔하고, 길이가 1짜리인 frequent itemset을 찾는다.
2. 찾은 frequent item보다 길이가 1 더 긴 itemset을 candidate로서 생성해낸다.
3. 만든 candidate를 DB에 적용해 필터링해 frequent한 itemset만 남긴다.
4. 조건을 만족하는 frequent pattern을 더 이상 찾을 수 없을 때까지 길이를 1씩 늘려가며 2,3,4를 반복한다.
즉, apriori는 Candidate Generation과 Test-Approach 으로 구성된 알고리즘으로 이해하면 되겠다.
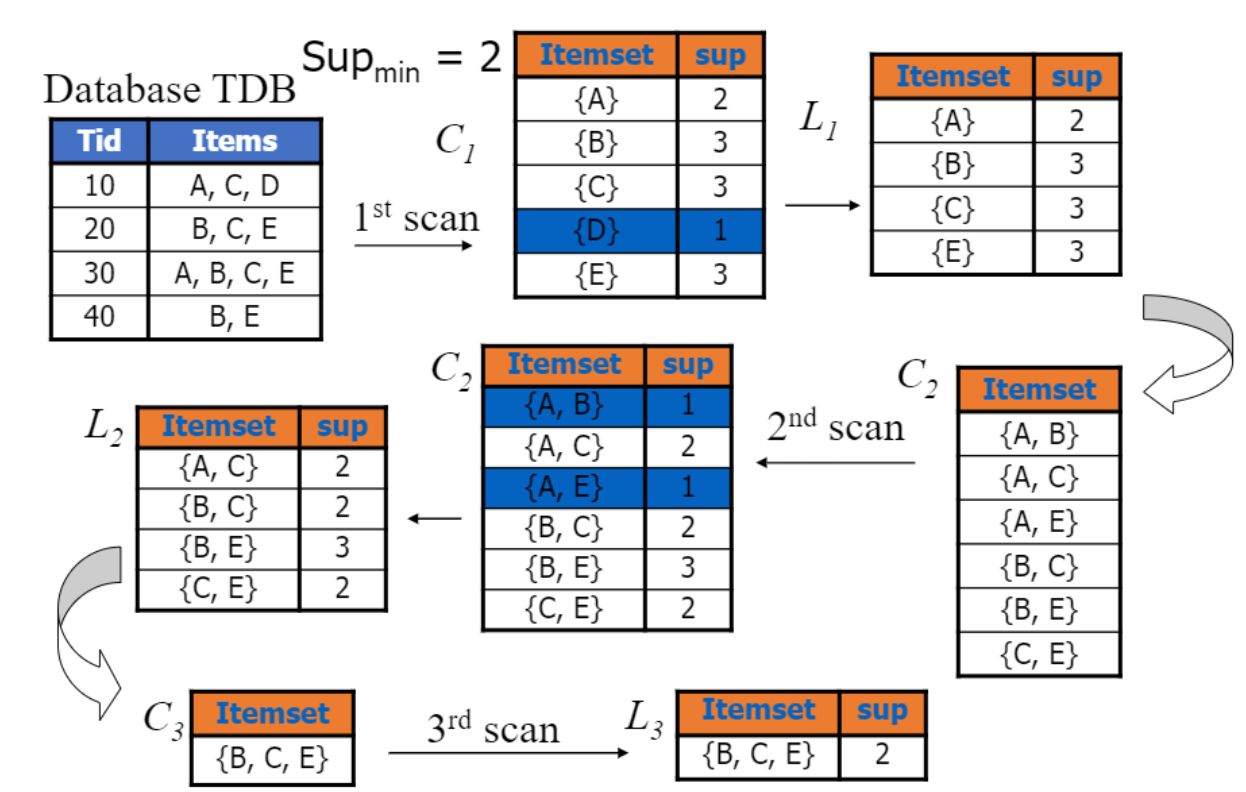
그림으로도 apriori 알고리즘을 이해해보자.
C는 candidate itemset, L은 C로부터 만든 frequent pattern output이다.
데이터베이스로부터, 길이가 하나짜리인 candidate C1를 만든다. (Candidate Generation)
(여기서는 모든 개별 product 집합이 각각의 itemset이 될 것이다.)
이어서 C1의 각 itemset이 전체 데이터 셋에서 얼마나 차지하는 지 계산하여, support를 만족하는 요소만 남긴다.(L1)
L1을 기반으로 두 번째 candidate C2를 만드는 것이 다음 단계가 될 것이다. (Candidate Generation)
L1의 itemset을 조합해 만들어질 수 있는 길이가 두 개짜리인 candidate들을 만든다.
여기서부터는, 만들어지는 candidate의 모든 부분집합이 (C_k+1), 이전 state의 frequent itemset(L_k)에 존재하는 지 확인하는 과정이 필요하다. (self-joining & pruning)
C2를 만들 때는, 만들어지는 길이가 2인 itemset의 모든 subset이 L1에 존재하고 있기 때문에 따로 더 조치하지 않고 넘어간다.
마찬가지로, C2의 각 itemset이 전체 데이터 셋에서 얼마나 차지하는 지 계산하여, support를 만족하는 요소만 남긴다.(L2)
C3를 만드는 과정을 눈여겨 보자.
이전 과정과 동일하게, L2를 기반으로 길이가 3짜리인 itemset들을 만든다.
{A, C} {B, C} {B, E} {C, E}
self-joining을 적용해 두 itemset의 합집합 중 길이가 3짜리인 후보집합들을 만든다.
{A, B, C} {A, C, E} {B, C, E}
만들어진 후보들의, 길이가 2짜리인 부분집합을 살펴보자.
{A, B, C}: {A, B} {A, C} {B, C}
{A, C, E}: {A, C} {A, E} {C, E}
{B, C, E}: {B, C} {C, E} {B, E}
L2에 없는 itemset인 {A, B}, {A, E}가 있는 후보는 pruning된다.
따라서, C3에 남는 itemset은 하나다.
{B, C, E}
C3의 각 itemset이 전체 데이터 셋에서 얼마나 차지하는 지 계산하여, support를 만족하는 요소만 남긴다. (L3)
L에 남은 itemset이 없을 때까지, itemset 길이를 하나씩 늘려가며 이 과정을 반복하는 것이 apriori다.
아래 pseudo-code를 읽으면서, 위 과정을 한 번 더 이해해보자.

Apriori의 중요한 Detail
candidate generation에서 기억해야 할 것은 두 가지다.
Candidate Generation
Counting Supports
Candidate Generation에서 빠뜨리지 않아야 하는 두 가지 step은 아래와 같다.
Self-joining
Pruning
Apriori Based Frequent Pattern Mining의 한계점과 극복법
Apriori의 한계점들을 살펴보자. 대부분은 비효율적인 면이다.
- transaction database를 여러 번 스캔해야 한다.
- candidate의 수가 너무 많다.
- candidate의 support를 세는 데 너무 많은 비용이 든다 등
이러한 한계를 극복하기 위한 방법으로는 아래 등이 있다.
- database scan의 횟수를 줄이기
- candidate의 수를 줄이기 등
'Data Science > Mining' 카테고리의 다른 글
| Mining Max-Pattern, Mining Closed Pattern (0) | 2022.04.01 |
|---|---|
| FP-Tree와 FP-Growth (0) | 2022.04.01 |
| Improving Apriori (0) | 2022.04.01 |
| Frequent Pattern Analysis의 기본 개념 (0) | 2022.03.25 |
| 데이터 마이닝 (Data Mining)의 개괄 (0) | 2022.03.24 |