😶 MLE(Maximum Likelihood Estimation)
아래 블로그 참고하여 작성
최대우도법(MLE) - 공돌이의 수학정리노트 (Angelo's Math Notes)
최대우도법(MLE) - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
✨likelihood

데이터를 샘플링 추출하였을때 위 그림처럼 나왔다고 가정
전체 분포를 추정한다고 했을 때 파란색 분포보다 주황색 분포일 가능성이 더 높음
⇒ 표본이 특정 데이터로부터 나왔을 가능도가 likelihood인 것.
⇒ ‘가능도’의 계산은 각 표본에 대한 확률밀도함수에서의 높이(likelihood)의 곱으로 구하는 것이 가능
✨‘maximum’ likelihood estimation
표본에 근거해 추정한 분포의 likelihood가 최대가 되도록 그 분포를 추정하는 방식을 의미!
보통 계산의 편의를 위해 log를 취한 log likelihood를 기준으로 함
-log likelihood를 최소화하는 것과 같음
⇒ likelihood가 최대가 되는 모델 파라미터 (θ)를 추정하는 방법
😶 Bayesian Theory
베이지안 이론
베이지안 이론 (Bayesian Theroy) 이란?
말도 많고 탈도 많은 베이지안. 머신러닝 이니 인공지능이니 이런것들이 뜰수록 덩달아 자주 사람들입에 오르 내리는게 베이지안(bayesian) 이다. 수식을 가지고 어렵게 이야기하지만, 기초적인
ddiri01.tistory.com
조건부 확률.
prior p(A) 과 likelihood p(B|A)를 안다면 posterior p(A|B)를 알 수 있다는 정리.
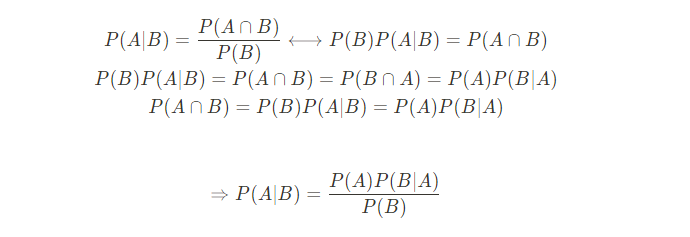
😶 Bayesian Optimization
베이지안 최적화 (아래 블로그 참고하여 작성)
Bayesian Optimization 개요: 딥러닝 모델의 효과적인 hyperparameter 탐색 방법론 (1) - 블로그 | 코그넥스
Bayesian Optimization 개요: 딥러닝 모델의 효과적인 hyperparameter 탐색 방법론 (1) - 블로그 | 코그넥스
Interpretable Machine Learning 개요: (1) 머신러닝 모델에 대한 해석력 확보를 위한 방법
www.cognex.com
하이퍼파라미터 튜닝방식 중 하나의 종류.
✨기존 하이퍼파라미터 튜닝방식들
2023.03.19 - [Data Science/ML | DL] - Learning Rate Scheduling과 Hyperparameter Tuning
Learning Rate Scheduling과 Hyperparameter Tuning
😶Learning Rate Scheduling 2023.03.06 - [Data Science/ML | DL] - Optimization: Gradient Descent를 넘어서 Optimization: Gradient Descent를 넘어서 Optimization에 대한 포스팅을 Gradient Descent 를 중점으로 했었다. 2022.08.21 - [Data S
dippingtodeepening.tistory.com
✔Manual Search
이전에 시도했던 하이퍼파라미터 조합, 값들을 넣었을 때 결괏값 변화에 근거해 manual하게 하이퍼파라미터를 바꿔가면서 최적 조합을 찾는 방식
⇒ 시간이 많이 걸리고 찾는다는 보장이 없음
✔Grid Search
하이퍼파라미터 특정 구간 내 후보들을 일정한 간격을 두고 선정해 모든 조합 경우의 수를 시도, 가장 성능이 좋은 조합을 선정
⇒ 탐색하고자 하는 범위 또는 하이퍼파라미터 개수가 많아질수록 시간이 기하급수적으로 증가
⇒ 특정 하이퍼파라미터가 다른 하이퍼파라미터보다 성능에 미치는 영향이 클 경우, 비교적 영향이 적은 하이퍼파라미터를 일정한 간격을 두고 모두 시도해보는 것이 시간낭비
✔Random Search
탐색 대상 구간 내의 후보 하이퍼파라미터 값들을 랜덤하게 샘플링(Random Samping)
간격 사이에 위치한 값들에 대해서도 확률적으로 탐색이 가능
불필요한 반복횟수를 대폭감소
⇒ 이전까지의 조사 과정에서 얻어진 hyperparameter 값들의 성능 결과에 대한 ‘사전 지식’이 반영되어 있지 않다는 점에서 불필요한 반복이 존재
✨Bayesian Optimization
매 회 새로운 hyperparameter 값에 대한 조사를 수행할 시 ‘사전 지식’을 충분히 반영하면서, 동시에 전체적인 탐색 과정을 체계적으로 수행할 수 있는 방법론
“하이퍼파라미터”에 대해 최적화를 진행한다고 이해하면 쉬움
✔베이지안 최적화를 위해 필요한 두 가지 요소
- Surrogate Model 현재까지 조사된 입력 하이퍼파라미터-Objective Function의 값 pair ((x, f(x)), (x2, f(x2)…)를 바탕으로 미지의 Objective Function을 확률적으로 추정하는 모델
- Acquisition Function
- 현재까지의 목적함수에 대한 확률적 추정 결과를 바탕으로 ‘최적 입력값을 찾는 데 있어 가장 유용한’ 다음 하이퍼파라미터 입력값 후보를 추천하는 모델

파란 실선: 실제 Objective Function
빨간 점: 관측한 하이퍼파라미터 값
검정 점선: 관측값을 바탕으로 Surrogate Model이 추정한 Objective Function
보라색 그래프 EI(x): 다음 하이퍼파라미터 후보 추천에 사용되는 Acquisition Function

새로운 하이퍼파라미터 후보 (x_n+1)와 Surrogate Model 업데이트를 번갈아 반복하여 진행 (pseudo code 참고)
최종 하이퍼파라미터로는 추정된 Objective Function을 최대로 만드는 값을 선택.
자세한 내용은 참고 블로그 읽어볼 것.
'Data Science > ML | DL' 카테고리의 다른 글
| Generative Model: Perceptual Loss와 Style Loss (1) | 2023.10.12 |
|---|---|
| Learning Rate Scheduling과 Hyperparameter Tuning (0) | 2023.03.19 |
| Optimization: Gradient Descent를 넘어서 (0) | 2023.03.06 |
| Training Technique: Regularization(규제) (0) | 2023.03.06 |
| Training Technique: Data Pre-processing, Weight Initialization, Feature Normalization (0) | 2023.03.05 |