데이터베이스에서 여러 패턴들을 mining하는 방법을 배웠다.
하지만, 방대한 크기의 데이터에서 모든 패턴을 찾는 것은 비현실적이다.
data mining은 interactive해야 하는데, 이는 즉 사용자가 무엇을 mining할지를 결정해야 한다는 소리다.
그런 의미에서, Constraint-Based Mining은 '무엇을 mining 할 것인지에 대해 제약(constraints)조건을 제공'해야 하는 것에 기안한다.
Constraint-Based Mining은, 효율적인 mining을 위한 constraints를 찾는 것을 의미한다.
데이터마이닝에서의 제약(Constraints)
여러가지가 있지만, Data Contraint는 SQL과 같은 쿼리(quries)문제로 생각하면 된다.
가령, '시카고'에 있는 '12월 21일'에 판매된 상품만을 찾는 것이 제약이 걸려있는 데이터에서의 패턴 mining문제라고 생각하면 된다.
이밖에도, min support와 min confidence를 어느 정도로 설정해야 할 지 등이 제약의 종류에 속한다.
Knowlege Type Constraint
Data Constraint
Dimension/Level Constraint
Interestingness Constraint
...
Anti-Monotonicity
itemset S가 제약(constraint)에 침해(violated)되었을 때, 그 superset도 당연히 제약을 만족하지 못하는 성질이다.
예를 들어보자.
sum(S.Price) ≤ v
위 constraint는 anti-monotone하다고 이야기한다.
itemset 집합 가격의 합이 v를 넘겼다고 했을 때, 여기서 itemset이 더해진다고 하더라도 constraint을 만족할 수 없다.
이미 가격의 합이 v를 넘겼고(violated), 가격이 음수인 경우는 없기 때문이다.
sum(S.Price) ≥ v
이 constraint의 경우, anti-monotone하지 않다고 이야기한다.
itemset 집합 가격의 합이 v를 넘기지 못했다고 했을 때, itemset이 계속 더해질 경우 constraint를 만족해버리는 상황이 올 수 있기 때문이다.
range(S.profit) ≤ 15
아래와 같은 profit 리스트가 주어졌을 때, 위 제약이 anti-monotone한지 확인해보자.

ab(0~40) 등 costraint를 violate하는 item들이 보인다.
여기서 ab의 superset을 만든다고 해서 constraint를 만족하는 경우가 생길 수 없기 때문에,
해당 constraint는 anti-monotone하다. (더해봤자 소용이 없다.)
Monotonicity
Anti-Monotonicity와 반대되는 성질이다.
itemset S가 제약을 만족(satisfies)할 때, 그 모든 superset도 당연히 제약을 만족하는 성질이다.
역시 예를 들어보자.
sum(S.Price) ≥ v
위에서 나온 예시다. (anti-monotone하지 않았던 예)
이 제약의 경우, monotone하다.
itemset의 가격 합이 v를 넘겼을 때, 당연히 거기서 item이 추가되어 superset이 생긴다고 하더라도 가격 합이 줄어들지는 않는다.
min(S.Price) ≤ v
이 제약도 monotone하다.
itemset 중 가장 가격이 낮은 녀석의 가격이 v보다 작을 때, item이 추가된다고 하더라도 제약을 어기는 일은 없다.
range(S.profit) ≥ 15
이 제약도 마찬가지로 monotone하다. (위 표 참고)
ab (0~40) 등 제약을 만족하는 itemset들이 있다.
여기서 ab에 어떤 item을 더해 superset을 더하더라도, 제약을 침해하는 경우는 없기 때문에 monotone하다고 이야기할 수 있다.
Succinctness
해당 제약조건을 만족시키는 모든 항목집합을 명확하게 생성가능한 제약이 가지는 성질이다.
itemset A1을 구성하는 모든 요소가 제약조건을 만족한다고 치자. 만약 다른 itemset S에 A1을 구성하는 요소가 하나라도 포함되어 있는 순간, S는 그 제약조건을 만족하게 되는 것이다.
다시 말해, 제약조건을 만족시키는 모든 항목집합인 A1이 있을 때, A1의 요소 하나만 있다면 어떤 조합이든 관계 없이, 해당 제약조건을 만족하는 itemset S를 간단히 계산(simply computed)할 수 있는 성질이다.
역시 예를 들어보자.
min(S.price) ≤ v
succinctness를 가지고 있다.
v보다 가격이 적은 상품 하나만 있으면, 어떤 조합이든 관계 없이 제약을 만족하기 때문이다.
sum(S.price) ≥ v
여기서는 succinctness가 있다고 말하기 어렵다.
요소 하나가 제약조건을 만족시키는지를 결정하는 것이 아니기 때문이다.
(제약조건을 만족시키는 항목집합을 명확하게 생성할 수 없음)
database를 살펴보지 않고도, itemset S가 제약을 만족하는지를 알아낼 수 있다는 점이 장점이다.
즉, constraint가 succinctness를 가지고 있다는 말은, support 계산 전이라도 해당 제약을 만족하는 항목집합을 명확히 생성할 수 있다는 말과 같다. (pre-counting pushable)
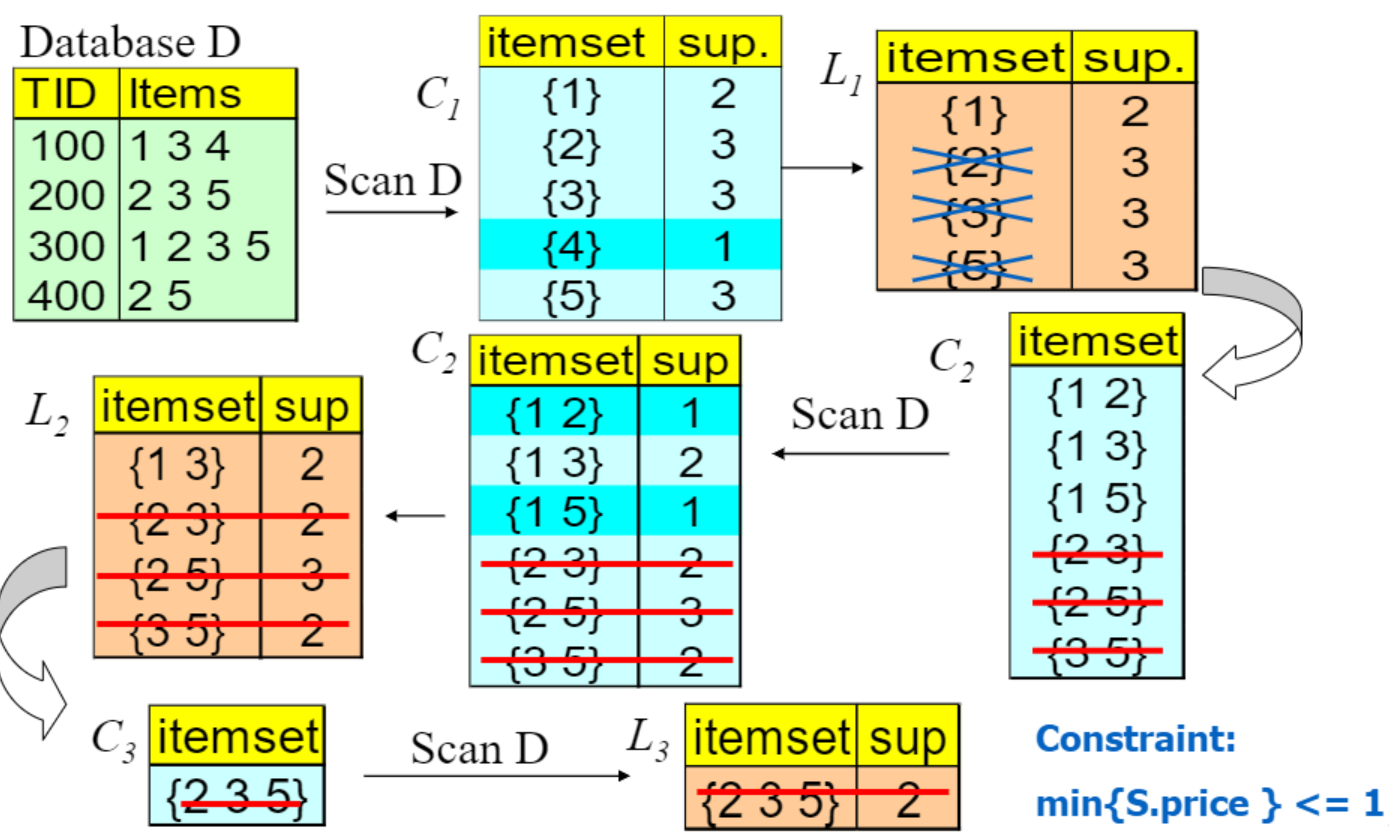
Apriori Algorithm으로 보는 제약의 성질들
위에서 설명한 constraint의 성질을 apriori에 적용해서 이해해보자.
[Naive Algorithm (Apriori + Constraint)]
먼저 단순히 apriori하고 constraint 적용(support)을 하는 것을 반복하는 경우다.

apriori대로 candidate를 만들고, testing한 후, item의 합이 5보다 같거나 큰 itemset을 지워주는 방식이다.
별로 효율적으로 보이지는 않는다.
[Constrained Apriori Algorithm: Anti-monotone Constraint Deep Pushing]
anti-monotone 성질을 활용한 apriori다.
해당 itemset이 제약조건을 침해하면, 그 모든 superset도 제약조건을 만족할 수 없다는 것을 이용한다.

candidate generation 단계에서, constraint를 침해하는 itemset을 지우는 것을 확인하자.
testing과정에서 해당 itemset이 애초에 만들어지지 않는 것을 확인할 수 있다.
[Constrained Apriori Algorithm: Succinct Constraint Deep Pushing]
succinct 성질을 활용한 apriori다.
testing 단계에서, itemset 중 제약조건을 만족하는 요소가 하나라도 있는 경우만 남긴다.
다음 candidate generation에서는, 해당 경우와 조합해서 만들 수 있는 길이 k+1짜리 itemset이 candidate가 될 것이다. (그림 참고)
'Data Science > Mining' 카테고리의 다른 글
| Rule-Based Classification & Associative Classification (0) | 2022.06.27 |
|---|---|
| Decision Tree (0) | 2022.06.27 |
| Association Rules Mining (0) | 2022.04.17 |
| Vertical Data Format으로 FP 찾기: CHARM (0) | 2022.04.17 |
| Mining Max-Pattern, Mining Closed Pattern (0) | 2022.04.01 |