벡터의 의미
일반적인 의미
벡터는 크기와 방향을 갖는다.
크기(magnitude) + 방향(orientation, direction)
*scalar(상수)는 magnitude만 있다.
선형대수에서의 의미
여러 개의 스칼라를 나열해 놓은 것으로 받아들일 수 있다.
$$vector x = [x1, x2, x3,,,, xn]$$
$$(x ∈ R^n)$$
x1, x2, x3 등을 벡터의 element 또는 component라 하며,
n개의 element로 이루어진 위와 같은 벡터를 통상적으로
실수집합으로 이루어진 n - dimensional(차원) vector
라고 부른다.
벡터의 표기
일반적으로 벡터는 아래와 같이 Column Vector Notation으로 표기한다.

*Row Vector Notation은 위의 그림을 Transpose 한 것이다. (전치)
벡터의 예시
1. 좌표
2. 카메라, 컬러 이미지 ( [R,G,B] )
3. 함수 (e.g. f(x1, x2, x3... xn)) 등
용어
Magnitude
벡터의 각 요소의 제곱을 모두 합한 것에 루트를 씌워 magnitude를 계산한다.
$$||x|| = \sqrt{\sum_{i = 1}{x_i^2}}$$
*|| ||는 magnitude의 단위이며, 놈(norm) 이라 부른다.
Orthogonality (직교)
두 벡터가 직각을 이루는 것을 직교한다고 한다.
직교하면 내적이 0이 된다.
$$x ⊥ y -> x · y = 0$$
벡터의 연산

일때,,
Addition, Substitution
벡터를 더하고 뺄 때는 같은 차원의 벡터여야 한다. (X ∈ R^n 이고 Y ∈ R^n)


*뺄셈도 마찬가지.
Scalar Multiplication
상수를 벡터에 곱할 때는 단순히 모든 요소에 곱해주면 된다.

Inner Product (내적)
일반적으로 알고있는 내적은 아래와 같다.
$$x · y = ||x|| * ||y|| * cos\theta$$
내적은 교환법칙이 성립한다.
$$x · y = y · x$$
벡터의 요소 측면에서 이를 다시 쓰면 다음과 같다.
$$x · y = \sum_{i = 1}^{n}{x_iy_i}$$
#내적과 투사

한 벡터의 끝에서 다른 벡터 방향으로 수선의 발을 내리는 것을 투사 (Projection) 라고 한다.
내적은 한 벡터 안에 다른 벡터 성분이 어느정도 있는지 파악할 수 있게 한다는 점에서 의미가 있다.
내적( ||a|| * ||b|| * cos(seta) ) = 한 벡터->다른 벡터로의 투사체 길이( ||b|| * cos(seta) ) X 다른 벡터의 길이( ||a|| )
Cross Product(외적)
일반적으로 알고있는 외적은 아래와 같다.
$$x × y = ||x|| * ||y|| * sin\theta$$
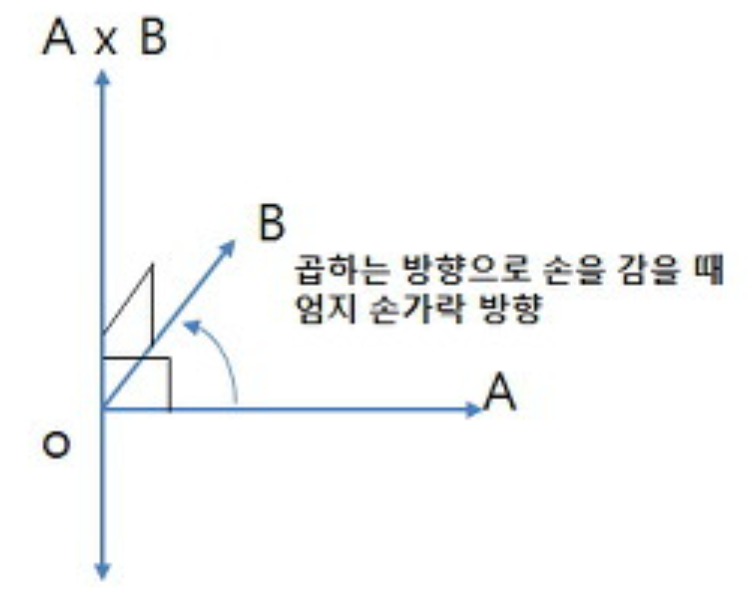
내적과 다르게, 외적은 교환법칙이 성립하지 않는다.
$$x × y = -y × x$$
벡터의 요소 측면에서 예를 들어 이를 다시 쓰면 다음과 같다.
$$x = \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix}, y = \begin{bmatrix} y_{1} \\ y_{2} \\y_{3} \\ \end{bmatrix}$$
이고,
$$i = \begin{bmatrix}
1 \\
0 \\
0 \\
\end{bmatrix},
j = \begin{bmatrix}
0 \\
1 \\
0 \\
\end{bmatrix},
k =
\begin{bmatrix}
0 \\
0 \\
1 \\
\end{bmatrix},
$$
i, j, k는 unit vector(magnitude 가 1이고 방향이 x, y, z축과 같은 벡터) 일때,
$$x × y = i(x2*y3 - x3*y2) + j(x3*y1 - x1*y3) + k(x1*y2 - x2*y1)$$
이다. 즉,
$$x × y = \begin{bmatrix}
x_{2} y_{3} - x_{3} y_{2} \\
x_{3} y_{1} - x_{1} y_{3} \\
x_{1} y_{2} - x_{2} y_{1} \\
\end{bmatrix}$$
참고: 내적의 결과는 scalar 이지만, 외적의 결과는 또다른 벡터 이다.
벡터와 벡터 간의 거리 (Distance)
벡터 간의 거리는 일반적으로 다음과 같이 나타낸다.
$$d = ||x - y|| = ||y - x||$$
벡터의 요소가 드러나도록 나타내면 다음과 같다.
$$L_2 norm = \sqrt{\sum_{i=1}^{n}{(x_i - y_i)^2}}$$
*L1 norm 은 L2의 제곱 대신 절댓값을 사용하여 계산한다.
*L∞ norm은 |xi - yi| 중 가장 큰 값이 결과다.
이러한 L1, L2, L∞를 cost function이라고도 부른다.
'수학 > 선형대수' 카테고리의 다른 글
| 가우스소거법(Gaussian Elimination)과 LU분해(LU Decomposition) (0) | 2021.10.09 |
|---|---|
| 선형결합(Linear Combination)과 연립일차방정식 (Linear System Equation) (0) | 2021.10.06 |
| 2X2 행렬의 역행렬에 관해 (0) | 2021.09.15 |
| 행렬(Matrix) (0) | 2021.09.15 |
| 선형성이란(Linearity) (0) | 2021.09.14 |